А образование уже ныряет в омуты...
Несмотря на то, что в школе педагогов 25-45 лет, то есть реально умеющих и могущих, осталось с гулькин нос, наши чиновники бодро рапортуют про успехи в изучении детишками школьных премудростей. Совмещая полезное с приятным, то есть ещё и зарабатывая кое-какие деньжата, специалисты областных управлений и республиканских департаментов штампуют разного вида олимпиады, результаты которых включают в разные оптимистические отчеты.
Вот только мало-мальски знающие люди давно сбежали и из разных институтов повышения квалификации, а оставшиеся перекладывальщики бумаг пытаются что-то подставить в старые материалы, стряхнуть пыль и выдать за новые блестящие идеи. В результате получаются конфузы. Возьмем, к примеру, добровольно-обязательные интернет-олимпиады, недавно спущенные на школы. Вот пример заданий по математике 8 класса, разработанные Минским областным институтом развития образования. Взял самые первые, то есть, самые легкие 3 задачки из заданных 15. Смотри скан.
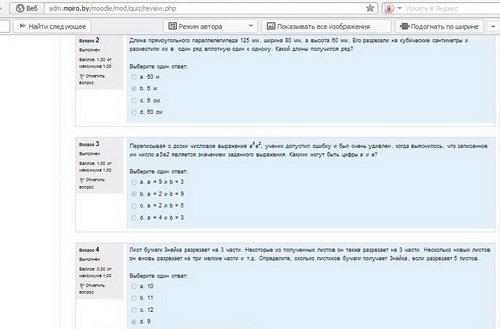
Задача 2. Длина прямоугольного параллелепипеда 125 мм, ширина 80 мм, а высота 60 мм. Его разрезали на кубические сантиметры и разместили их в один ряд вплотную один к одному. Какой длины получился ряд. Выберите один ответ: а) 60 м b) 6 м с) 6 см d) 60 см.
"Разрезали на кубические сантиметры" - уже весело, хорошо, что не на градусы. Особенно, если учесть, что длина 12,5 см. Судя по ответам, автор предлагает не только "разрезать на кубические сантиметры", но ещё и слепить остатки "из того, что было".
Задача 3. Переписывая с доски числовое выражение a5b2, ученик был очень удивлен, когда выяснилось, что записанное им число a5b2 является значением заданного выражения. Какими могут быть цифры a и b? Выберите один ответ: a) a=9, b=3 b) a=2, b=9 c) a=2,b=5 d) a=4, b=3
Я, признаться, читая задание и сопоставляя ответы, удивился не меньше описанного ученика. Как бы объяснить уважаемым методистам, что в математике выражение a5b2 обозначает не четырехзначное число (для этого рисуют над числом горизонтальную линию), а произведение четырех множителей. Я уже молчу, что а5b2 обозвано значением выражения.
Задача 4. Лист бумаги Знайка разрезает на три части. Некоторые из полученных листов он вновь разрезает на три мелкие части и так далее. Определите, сколько листиков бумаги получит Знайка, если разрезает 5 листов. Выберите один ответ: a) 10 b) 11 c) 12 d) 9
Ну а тут до чего доколебаться? До сущего пустячка -- Знайка может получить любое нечетное число листиков, не меньшее 5. То есть правильных ДВА ответа, а приказано выбрать один. Ученика с теорией вероятности знакомят, что ли? Или приучают будущего участника "Суперлото" к счастливому билетику.
Продолжать не буду, смысл поста понятен. Какие олимпиады, какое стимулирование деградирующих школьников, если доброе-вечное вкладывают недавние абитуриенты с 10 баллами из 100 по ЦТ или ничего хорошего уже не ждущие пенсионеры. И так везде - от сельской школы до академий. "Потеряли учителя, ходим дурныя".